Cross validation is an essential tool in statistical learning 1 to estimate the accuracy of your algorithm. Despite its great power it also exposes some fundamental risk when done wrong which may terribly bias your accuracy estimate.
In this blog post I’ll demonstrate – using the Python scikit-learn2 framework – how to avoid the biggest and most common pitfall of cross validation in your experiments.
Theory first
Cross validation involves randomly dividing the set of observations into k groups (or folds) of approximately equal size. The first fold is treated as a validation set, and the machine learning algorithm is trained on the remaining k-1 folds. The mean squared error is then computed on the held-out fold. This procedure is repeated k times; each time, a different group of observations is treated as a validation set.
This process results in k estimates of the MSE quantity, namely $MSE_1$, $MSE_2$,…$MSE_k$. The cross validation estimate for the MSE is then computed by simply averaging these values:
$$CV_{(k)} = 1/k \sum_{i=1}^k MSE_i$$
This value is an estimate, say $\hat{MSE}$, of the real $MSE$ and our goal is to make this estimate as accurate as possible. $MSE$ is just one for the possible metrics you can estimate using cross validation but the results of this blog post are independent from the type of metric you use.
Hands on
Let’s now have a look at one of the most typical mistakes when using cross validation. When cross validation is done wrong the result is that $\hat{MSE}$ does not reflect its real value $MSE$. In other words, you may think that you just found a perfect machine learning algorithm with incredibly low $MSE$, while in reality you simply wrongly applied CV.
I’ll first show you – hands on – a wrong application of cross validation and then we will fix it together. The code is also available as an IPython notebook on github.
Dataset generation
|
1 2 3 4 5 6 7 8 9 |
# Import pandas import pandas as pd from pandas import * # Import scikit-learn from sklearn.linear_model import LogisticRegression from sklearn.cross_validation import * from sklearn.metrics import * import random |
To make things simple let’s first generate some random data and let’s pretend that we want to build a machine learning algorithm to predict the outcome. I’ll first generate a dataset of 100 entries. Each entry has 10.000 features. But, why so many? Well, to demonstrate our issue I need to generate some correlation between our inputs and output which is purely casual. You’ll understand the why later in this post.
|
1 2 3 4 5 6 7 |
np.random.seed(0) features = np.random.randint(0,10,size=[100,10000]) target = np.random.randint(0,2,size=100) df = DataFrame(features) df['target'] = target df.head() |
Feature selection
At this point we would like to know what are the features that are more useful to train our predictor. This is called feature selection. The simplest approach to do that is to find which of the 10.000 features in our input is mostly correlated the target. Using pandas this is very easy to do thanks to the corr() function. We run corr() on our dataframe, we order the correlation values, and we pick the first two features.
|
1 2 3 4 5 6 7 8 9 10 |
corr = df.corr()['target'][df.corr()['target'] < 1].abs() corr.sort(ascending=False) corr.head() # 8487 0.428223 # 3555 0.398636 # 627 0.365970 # 3987 0.361673 # 1409 0.357135 # Name: target, dtype: float64 |
Start the training
Great! Out of the 10.000 features we have been able to select two of them, i.e. feature number 8487 and 3555 that have a 0.42 and 0.39 correlation with the output. At this point let’s just drop all the other columns and use these two features to train a simple LogisticRegression. We then use scikit-learn cross_val_score to compute $\hat{MSE}$ which in this case is equal to 0.249. Pretty good!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
features = corr.index[[0,1]].values training_input = df[features].values training_output = df['target'] logreg = LogisticRegression() # scikit learn return the negative value for MSE # http://stackoverflow.com/questions/21443865/scikit-learn-cross-validation-negative-values-with-mean-squared-error mse_estimate = -1 * cross_val_score(logreg, training_input, training_output, cv=10, scoring='mean_squared_error') mse_estimate # array([ 0.45454545, 0.2, 0.2, 0.1, 0.1, # 0., 0.3, 0.4, 0.3, 0.44444444]) DataFrame(mse_estimate).mean() # 0 0.249899 # dtype: float64 |
Note [1]: I am using $MSE$ here to evaluate the quality of the logistic regression, but you should probably consider using a Chi-squared test. The interpretation of the results that follows is equivalent.
Note [2]: By default scikit-learn use Stratified KFold3 where the folds are made by preserving the percentage of samples for each class.
Knowledge leaking
According to the previous estimate we built a system that can predict a random noise target from a random noise input with a $MSE$ of just 0.249. The result is, as you can expect, wrong. But why?
The reason is rather counterintuitive and this is why this mistake is so common4. When we applied the feature selection we used information from both the training set and the test sets used for the cross validation, i.e. the correlation values. As a consequence our LogisticRegression knew information in the test sets that were supposed to be hidden to it. In fact, when you are computing $MSE_i$ in the i-th iteration of the cross validation you should be using only the information on the training fold, and nothing should come from the test fold. In our case the model did indeed have information from the test fold, i.e. the top correlated features. I think the term knowledge leaking express this concept fairly well.
The schema that follows shows you how the knowledge leaked into the LogisticRegression because the feature selection has been applied before the cross validation procedure started. The model knows something about the data highlighted in yellow that it shoulnd’t know, its top correlated features.
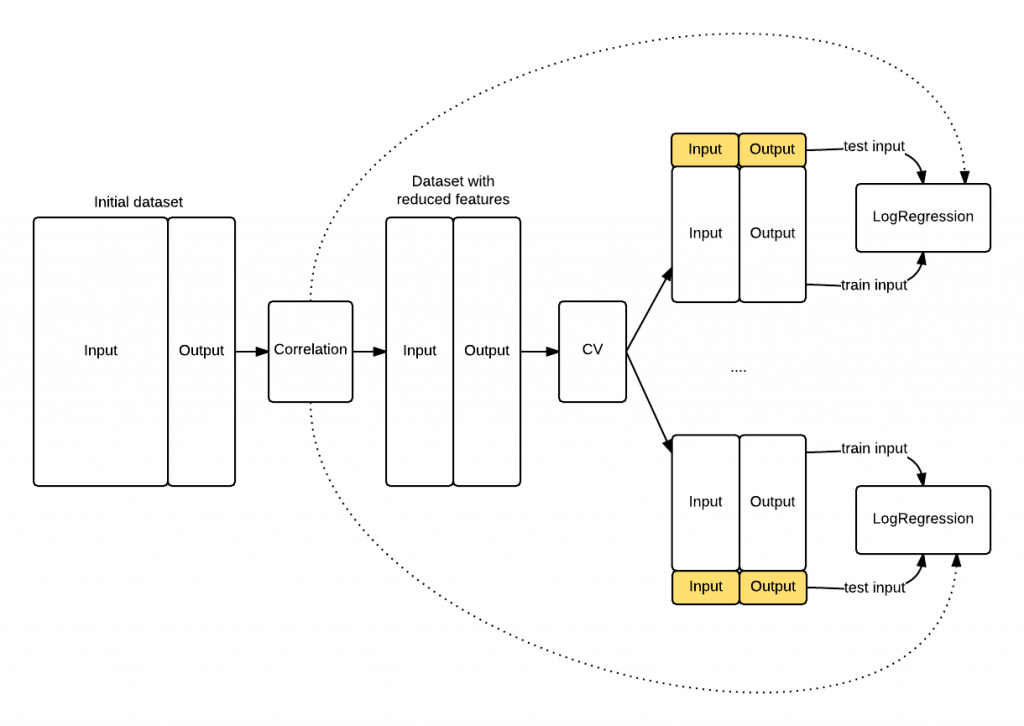
Proof that our model is biased
To check that we were actually wrong let’s do the following:
* Take out a portion of the data set (take_out_set).
* Train the LogisticRegression on the remaining data using the same feature selection we did before.
* After the training is done check the $MSE$ on the take_out_set.
Is the $MSE$ on the take_out_set similar to the $\hat{MSE}$ we estimated with the CV? The answer is no, and we got a much more reasonable $MSE$ of 0.53 that is much higher than the $\hat{MSE}$ of 0.249.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
take_out_set = df.ix[random.sample(df.index, 30)] training_set = df[~(df.isin(take_out_set)).all(axis=1)] corr = training_set.corr()['target'][df.corr()['target'] < 1].abs() corr.sort(ascending=False) features = corr.index[[0,1]].values training_input = training_set[features].values training_output = training_set['target'] logreg = LogisticRegression() logreg.fit(training_input, training_output) # LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, # intercept_scaling=1, max_iter=100, multi_class='ovr', # penalty='l2', random_state=None, solver='liblinear', tol=0.0001, # verbose=0) y_take_out = logreg.predict(take_out_set[features]) mean_squared_error(take_out_set.target, y_take_out) # 0.53333333333333333 |
Cross validation done right
In the previous section we have seen that if you inject test knowledge in your model your cross validation procedure will be biased. To avoid this let’s compute the features correlation during each cross validation batch. The difference is that now the features correlation will use only the information in the training fold instead of the entire dataset. That’s the key insight causing the bias we saw previously. The following graph shows you the revisited procedure. This time we got a realistic $\hat{MSE}$ of 0.44 that confirms the data is randomly distributed.
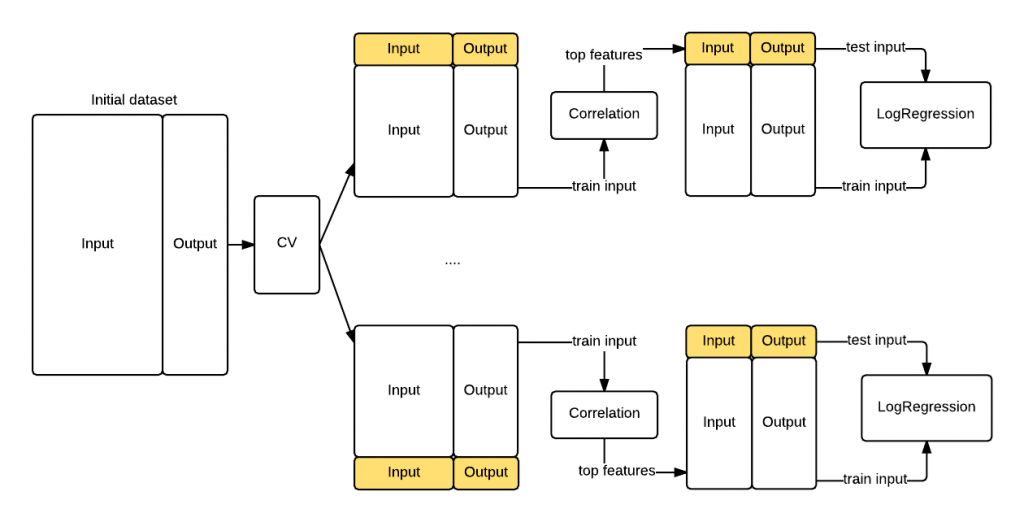
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
kf = StratifiedKFold(df['target'], n_folds=10) mse = [] fold_count = 0 for train, test in kf: print("Processing fold %s" % fold_count) train_fold = df.ix[train] test_fold = df.ix[test] # find best features corr = train_fold.corr()['target'][train_fold.corr()['target'] < 1].abs() corr.sort(ascending=False) features = corr.index[[0,1]].values # Get training examples train_fold_input = train_fold[features].values train_fold_output = train_fold['target'] # Fit logistic regression logreg = LogisticRegression() logreg.fit(train_fold_input, train_fold_output) # Check MSE on test set pred = logreg.predict(test_fold[features]) mse.append(mean_squared_error(test_fold.target, pred)) # Done with the fold fold_count += 1 print(DataFrame(mse).mean()) # Processing fold 0 # Processing fold 1 # Processing fold 2 # Processing fold 3 # Processing fold 4 # Processing fold 5 # Processing fold 6 # Processing fold 7 # Processing fold 8 # Processing fold 9 DataFrame(mse).mean() # 0 0.441212 # dtype: float64 |
Conclusion
We have seen how doing features selection at the wrong step can terribly bias the $MSE$ estimate of your machine learning algorithm. We have also seen how to correctly apply cross validation by simply moving one step down the features selection such that the knowledge from the test data does not leak in our learning procedure.
If you want to make sure you don’t leak info across the train and test set scikit learn gives you additional extra tools like the feature selection pipeline5 and the classes inside the feature selection module6.
Finally, if you want know more about cross validation and its tradeoffs both R. Kohavi7 and Y. Bengio with Y. Grandvalet8 wrote on this topic.
If you liked this post you should consider following me on twitter.
Let me know your comments!
References
- Lecture 1 on cross validation – Statistical Learning @ Stanford
- Scikit-learn framework
- Stratified KFold Documentation
- Lecture 2 on cross validation – Statistical Learning @ Stanford
- Scikit-learn feature selection pipeline
- Scikit-learn feature selection modules
- R. Kohavi. A study of cross-validation and bootstrap for accuracy estimation and model selection
- Y. Bengio and Y. Grandvalet. No unbiased estimator of the variance of k-fold cross-validation
To do feature selection inside a cross-validation loop, you should really be using the feature selection objects inside a pipeline:
http://scikit-learn.org/stable/auto_examples/feature_selection/feature_selection_pipeline.html
http://scikit-learn.org/stable/modules/feature_selection.html
That way you can use the model selection tools of scikit-learn:
http://scikit-learn.org/stable/modules/model_evaluation.html
And you are certain that you won’t be leaking info across train and test sets.
Thank you Gael! This is a great insight, I will add your suggestion!
Your mathjax/latex isn’t rendering properly for many of the $MSE$ references… 🙂
Thank you Clay! Fixed now
Thanks for this – I enjoyed reading it. I think it would help to set your random seed in the beginning, though so that people running your notebook end up with the same data as you…
Thank you Fabian. You are absolutely right, I’ll do it.
Nice write-up!
Maybe add a short sentence about stratified k-fold cross-validation (default for classification estimators in scikit-learn).
Another note: If you want to evaluate the goodness of fit of a logistic regression model (in contrast to predictive performance measures like accuracy, classification error etc.), isn’t it more appropriate to use chi-square or mean deviance rather than mean squared error?
Thank you for you comment Sebastian. I think you are right, a chi-square is more appropriate. I’d say that for clarity using the MSE is more effective (everyone knows it), but I’ll point that out in the code for people to be aware.
I’ll also point out stratified k-fold
Very interesting read!
I would like to stress another requirement for the application of cross validation though that you may want to add: statistical independence of the samples in the data-set.
A quick example: Two scenarios
1) classification of images, randomly taken from the web
2) classification of images, extracted from a video stream
In the first scenario the images are independent of each other and we can apply cross validation to obtain a reliable performance of our system. However, the situation changes in the second setting: Subsequent images from a video are highly correlated and therefore not statistically independent anymore!
Say we extracted 100 images from the video, split those into 10 folds, and run through a cross-validation. If we predict an image i, what is the chance that the (very similar) adjacent frames i-1 or i+1 are in the training-set? It is 99%! In the second setting we are basically only testing how well we can preserve the pairwise similarity of images, which does not generalise at all to any realistic setting and biases our performance, our choice of features and choice of classification approach. This is a significant issue that many people are not aware of!
We just got a paper accepted in Ubicomp 2015 on this bias of cross-validation in time-series data and how it can be alleviated through a slightly adapted approach. I can’t share a link yet as the proceedings are not yet online, but drop me an email though if you are interested.
That’s a very nice example, Nils,
but if you are using logistic regression like shown in this post, don’t you make the assumptions that samples are i.i.d. anyway (i.e., in the likelihood function / or the reversed cost function if you will)? Aside from violated assumptions during model training, I think this — samples from different populations — is a problem in general, and k-fold cross validation is probably less affected than the holdout method.
I am looking forward to give your paper a read, this sounds interesting!
Cheers,
Sebastian
I would like to read that paper. Can you send it to alind_sap@yahoo.com . I am currently in the process of doing classification from images coming through video stream and was thinking how to appropriately test/Cross-Validate it. Should I take a totally new stream etc.
Great post. Nils, I will be interested in reading your article on cross validation and time series data (bikiengasalif@yahoo.fr).
Cheers,
Sure, most approaches in ML assume that the data is i.i.d. Lack of independence doesn’t lead to a bloated, biased performance of the methods though. Instead their performance is often disappointingly bad, as you waste a lot of parameters in modeling invariances or symmetries (e.g. translation in images). This is one of the reasons why convolutional networks work much better than fully connected networks in computer vision tasks.
You are right about the difference in populations being crucial in the evaluation. But in cases of non-i.i.d. data I would actually recommend hold-out validation over cross-validation. It all depends on how you select your folds. For example, using the last 20 images from the video example above as test-set wouldn’t suffer from the same degree of bias than cross-validation, as subsequent images are kept together in the same set.
Cheers
Nils
Thank you for sharing Nils, this is indeed a great example of another way to invalidate CV!
” For example, using the last 20 images from the video example above as test-set wouldn’t suffer from the same degree of bias than cross-validation, as subsequent images are kept together in the same set.” I agree in this case, I didn’t think about the time-series example specifically but assume that you were shuffling the training dataset prior to splitting.
Thanks for writing this. I’d like to comment that your “Theory first” section may confuse newcomers a little, since you make it sound as if cross-validation is intrinsically tied to MSE, whereas you can use it for various figures of merit. So, even if you want to use MSE as a “simple” example (though for a newcomer it might not be obvious), perhaps you could make it clearer that MSE is just one possible measurement?
(Also I agree that stratified crossval would be the next thing to introduce. A future post maybe…)
Thank you for your comment Dan. This is a good point, I’ll add a note to the section.
Noob question: if you then wanted a classifier for future data, which feature set should you use?
Hello Michael, thank you for your question.
In this particular example the learning automatically select the most correlated features so don’t need to choose between any of them.
In a real world setting where you want to select some features it is important that you take an hold-out set.
The hold-out set will be used to asses if the performance estimated by the CV has been biased by your feature selection (like in the example I gave here).
Make sense?
Nice post and very interesting!
After cross-validation we have got ten different models (k=10) and probably with a different feature selection. Which of these 10 models should be considered as the final model.
Thanks in advanced and sorry if it is a noob question.
Hello Pedro, thank you for your question!
it’s usually a good advice to select more than one model and average their predictions. In this example we got 10 models and we may decide to pick up the top 3 performers. This is because each of these models are biased towards one of the subsets they have been trained on and when you will see new data you actually don’t know which of them will perform best. Make sense?
Hi Alfredo
Can you please elaborate some more on the question that Michael asked. Which features to take in the final model?
Hi Vivek, thank you for your question.
the top performing model at the end of the CV will have some features selected. You can pick these.
If you want to be more conservative, you can look at the top 20% performers and see what features they selected and take these.
Remember that CV is a method to estimate the performance of a model. This includes both the feature selection procedure and the model training on these features.
So at the end you don’t just walk away with the top features, but both feature and the parameters of the Logistic regression associated with them.
Does it make sense?
Great post, it’s really helpful for someone just starting in ML like me.
Really appreciate that you are taking your time for replying to each comment. They are equally helpful as the post.
Glad you enjoyed Akhil!
Hi Alfredo!! First of all thanks a lot for the post 🙂 I was applying wrong cross validation in my reasarch. I have a question I hope you can answer me because I was not able to find the asnwer, I will add here a link to the post I did in sackoverflow.
https://stackoverflow.com/questions/45689181/how-to-implement-feature-selection-and-oversmpling-using-k-cross-validation
I’m trying to apply dimensionality reduction and oversampling for a dataset the one is imbalanced. For that purpose I use k-cross validation with 10 folds, and as I understood in your post I have to apply it when I perform the loops of the cross-validation. Do i have to apply the oversampling inside of the loop too? And in the case i have to, in which order do I have to apply it? I mean, inside of the loop I would apply first feature selection, then oversampling, and finally the classification algorithm?
I’m obtaining a poor result with the classifier and I think it can be cause I’m doing it wrong.
Hi Daniel, I am glad you liked the post.
I think oversampling is not related to the problem of validating the accuracy of the classifier (which is what cross validation is for) and so I would place it outside the loop.
Regarding the k-folds and your poor performance; if your problem is really unbalanced I would make sure that every fold get a representative percentage of both populations.
Make sense?
have a nice day!
Hi alfredo,
I was reading this post and doing the oversampling as he does.
http://www.marcoaltini.com/blog/dealing-with-imbalanced-data-undersampling-oversampling-and-proper-cross-validation
I’m applying in the moment undersampling and then oversampling inside of the cross validation loop. How would you do it or apply it outside of the loop? I was not able to find an example in internet related to my case, with dimensionality reduction and resampling in cross validation at the same time.
thanks!!
Hi Daniel,
I read the blog you pointed and Marco has a really good point so I would stick to what he suggests. I was a bit naive in my suggestion to do oversampling outside even though my assumption was also to perturbate the values a bit (which would maybe tame the problem highlighted by Marco).
I don’t understand what’s your issue with dimensionally reduction at that point. That must definitely be done inside the loop and I don’t see how oversampling should affect that. If in doubt I would do dim reduction before (just to avoid the perils of the artificially generated data)
make sense?
have a nice day,
Alfredo
Hi,
I apologise in advance for the necro-posting 🙂
I have a problem with your second pipeline. I don’t think that the 2nd pipeline is correct for doing what is intended. Or maybe it’s just that I don’t understand the main purpose 🙂
In fact I think that both of them are failing in the same way. In neither, feature selection plays any role (I understand that it’s just an example to prove a point but still.. 🙂 )
CV has to be used for model selection (hyperparameter opt.) and neither one does it correctly. Normally after a CV guided model selection, you have to refit all of the data as you’ll lose real information.
After saying that I’ll elaborate:
1st pipeline:
What’s the mse score obtained by CV on the 2 featured data.
So what’s being done is that, main data is reduced to 2 features and than checked how well this new matrix can represent our label. So here it’s kind of a choice. If after the correlation, CV was used to test for example if intercept will be enabled or not, it would be okay. But there is no comparison here. An assumption has been made here and CV has no real purpose but to provide a number.
And it’s true that as corr. analysis has been done beforehand results still may be biased.
I’m saying maybe, because I don’t think that your proof is solid. Because you’re proposing the following comparison:
a- Check CV-score on a 2*100 matrix to check 100 labels (0.29ish)
b- Check a score (not CV) on a sample most probably taken randomly from the set and use the remaing to train and evaluate the MSE.
2 completely different problems are compared here.
Depending on that 1 sample, it’s entirely possible to obtain for example b = 0.0004 or b = 1. It depends on the proportion and instance of data selected.
Essentially when you check like that you’re throwing the averaging power of the CV. You’re just looking at 1 sample where your model’s possibly overfitting so it’s failing on the test set (assuming that training scores are good).
Btw, I think that modelling 100 values with a 2*100 dataset, as values are random, it’s perfectly possible to obtain a MSE of 0.29. Generating infinite features doesn’t change a thing. You’re selecting the 2 most meaningful features anyway. If it’s not about selecting the most powerful 2 features, but to prove a point on statistical significance then feature selection was used wrongly as then it won’t be the point.
2nd pipeline:
This pipeline is proposed as a solution to the first pipeline. What was said is that our feature selection was biased in the first. Which means that our goal is to select the best 2 features (which appearently is a another choice made here) to represent our label.
However in the 2nd pipeline what’s represented isn’t doing that. Doing feature selection inside a CV pipeline means that for each fold it’s possible to take (and with 10000 features it’s most certainly is!) different features. So when averaging you’re averaging completely different things!
What had to be done was to loop, so that some combinations (for a complete search every 2 combinations of 10000 features) are put through CV. Which means that feature selection must be before CV and must be used to reduce possible combinations! So an example can be to use correlation information between features (not with the label) to remove highly correlated features.
So I think that the main problem here is not that CV was done wrong, it’s that the problem wasn’t clear. CV wasn’t used in a wrong way but used for a wrong reason, and also correlation analysis was also done for a wrong reason.
So it’s possible that the 1st pipeline may be biased, but the 2nd pipeline is just random calculations which have no meaning.
One might argue that the point IS to use different features for modelling different sample sets and combine them into one model but I suspect it’d perform extremely bad when a new point is added. And chosing a 3rd batch to test CV would be losing too much information.
Best regards.
Hi Xalron, really thank you for your feedback.
I will have to go back to your comment, double check in details and amend appropriately.
Independently from that, it would be helpful to get an amended version of the code with your comments applied, that would definitely make my job easier!
Thank you, have a nice day
Thanks for the post! So, the lesson learned here is that if you want to perform feature selection, this should be done after cross-validation? I am not sure if I agree. What if we use only the training set for feature selection? This way, knowledge from the test set wouldn’t leak.
Thank you Fernando!
Not after, but in the loop of CV, see the comparison between the first and the second diagram in the post
How? the test set will still use a reduced number of features if you do so, no? That’s the leak.
Looking forward to hearing back!